Kuliah Umum: LINGKARAN DAN SEGI TAK TERHINGGA

Kuliah Umum:LINGKARAN

DAN SEGI TAK TERHINGGA

Hendra GunawanCampus Center ITB, 18 April 2015

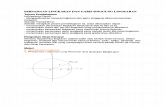
Yang Mana Lingkaran, danYang Mana Segi Tak Terhingga?

0 ½ 1¼ 81

18 April 2015 2(C) Hendra Gunawan

18 April 2015 (C) Hendra Gunawan 3

metro.co.uk

LINGKARAN


Beberapa sifat istimewa lingkaranyang diketahui saat ini antara lain:• Di antara bangun datar yang luasnya

sama, lingkaran mempunyai kelilingminimum.

• Lingkaran merupakan bentuk yang cocok untuk penutup lubang saluranair (ia takkan jatuh ke lubangnya).

Sejak 2500 tahun silam, bentuk lingkaran dianggapsebagai bentuk yang paling sempurna.

dev.physicslab.org

Apa yang Diketahui Orang Mesir Kunodan Babilonia tentang Lingkaran

Mesir Kuno (~1650 SM):Luas = (4/3)4r2.

Babilonia (~1000 SM):Keliling = 50r/8.

r


Temuan Archimedes (287-212 SM)tentang Lingkaran

Luas = Kr2, denganK = keliling : diameter ≈ 22/7.

Archimedes menaksir K dengan segi-96 beraturan(mulai dgn segi-6, lalu segi-12, segi-24, segi-48, danakhirnya segi-96 beraturan).

r


Archimedes juga menemukan rumus volume dan luas permukaan bola.

Bilangan π (BC, before calculator*)

Lambang bilangan π pertama kali dipakai olehWilliam Jones pada 1706.

π = keliling : diameter.

Mesir Kuno: π ≈ (4/3)4 ≈ 3,16.Babilonia: π ≈ 25/8 = 3,125.Archimedes: π ≈ 22/7 ≈ 3,14.


Bilangan π (AD, after decimals*)

π ≈3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067082148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420198938095257201065485863278865936153381827968230301952035301852968995773622599413891249721775283479131515574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012858361603563707660104710181942955596198946767837449448255379774726847104047534646208046684259069491293313677028989152104752162056966024058038150193511253382430035587640247496473263914199272604269922796782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955321165344987202755960236480665499119881834797753566369807426542527862551818417574672890977772793800

Claudius Ptolemy

Zu Chongzi

Al-Khasi

Christoph Grienberger

Madhava

Gottfried W. Leibniz

Isaac Newton

John Machin

Daniel Ferguson

Yasumada Kanada

Shigeru Kondo12,1 triliun angka(2013)


1 1 1arctan1 1 ...4 3 5 7π= = − + − +

33r

Berapa Banyak Sisi dan Titik Sudut(a) Persegi (b) Lingkaran

4 sisi, 4 titik sudut ??


Apakah Lingkaran MempunyaiTak Terhingga Sisi dan Titik Sudut?

titik sudut?

bukan titik sudut?

satu sisi?

tak terhingga sisi?

½

Apa yang dimaksud dengan sisi dan titik sudut?18 April 2015 10(C) Hendra Gunawan

Kita Perlu Definisi Sisi dan Titik Sudutuntuk Bangun Datar Sembarang*

*KECUALI:


Berapa Banyak Sisi dan Titik Sudut

4 sisi, 4 titik sudut







Sisi

• Bangun datar yang kita bahas dikelilingi olehsuatu lintasan tertutup sederhana yang ke-banyakan terdiri dari sejumlah kurva mulus.


• Sebagai contoh, bangun persegidikelilingi oleh suatu lintasan yang terdiri dari dari 4 kurva mulus, sementara lingkaran hanya terdiridari 1 kurva mulus.

• Nah, kurva-kurva mulus itulah yang kemudian kitadefinisikan sebagai sisi-sisi bangun datar tersebut.

Titik Sudut

• Di titik lainnya yang bukan titik singular, lintasannyamulus, tidak patah. Di sekitar titik ini, walau kurva-nya melengkung, ia sangat mirip dengan garis lurus tidak membentuk sudut!


• Pada bangun datar yang dikelilingi olehsuatu lintasan yang terdiri sejumlahterhingga kurva mulus, titik sudutadalah titik singular pada lintasan tsb.

• Di titik singular, lintasannya tidak mulus tetapi‘patah’ alias membentuk sudut (bukan 180o).

titik singular

Menghitung Banyak Sisidan Titik Sudut









Lingkaran hanya mem-punyai 1 sisi dan tidakmempunyai titik sudut.

Mark Twain: A circle is a round straight line with a hole in the middle.

Bangun Apa Ini?

0 ½ 1¼ 81

Let’s zoom8x


Apa ygterjadidi sini?

Bangun Apa Ini?


0 641

81

161

321

Hasilzoom 8x

SEGI TAK TERHINGGABangun inimemiliki takterhingga sisidan tak ter-hingga titiksudut.Tetapi, apakahO merupakantitik sudut?

0 ½ 1¼ 81


Definisi Titik Sudut dan Sisiyang Lebih Umum

Pertama kitaidentifikasi

setiap titik padalintasan tepi:

apakah iamemiliki rank 0

atau rank 1.

rank 1 rank 0

ϒ

Titik x є ϒ memiliki rank 1apabila ϒ mempunyai garissinggung di titik x tersebut.

Bila tidak, maka x memilikirank 0 (titik singular).



Selanjutnya, kitadefinisikan relasi

ekuivalen di antaradua titik yang

memiliki rank 1: A ~ B apabila kita dapat

menelusuri ϒ dari A keB tanpa melalui titik

yang memiliki rank 0.

rank 1

ϒ

rank 1

A B

A ~ B

Sisi yang memuat A didefinisikansebagai:{P є ϒ | P memiliki rank 1 dan P ~ A}

Jika A ~ B, maka sisi yang memuat A identik dengan sisi yang memuat B.



Ada duakemungkinan utk

titik yang memilikirank 0: atau

merupakan titiksudut, atau titik

singular yang tidakmembentuk sudut.

0 ½ 1¼ 81

O bukantitik sudut!


Bagaimana dengan Bangun Ini?

0 ½ 1¼ 81

161

Titiksudut

O jugatitik sudut!

tak terhinggabanyaknya


y = √x

Kasus Menarik pada Segi Tak Terhingga

O memiliki rank 1, tapi terisolasi!



TITIK PADA TEPI BANGUN DATAR

MEMILIKI RANK 1

MEMILIKI RANK 0

BAGIAN DARI SISI YANG MEMILIKI PANJANG POSITIF

TERISOLASI; “SISI YANG MEMILIKI PANJANG NOL”

BUKAN TITIK SUDUT

TITIK SUDUT

Serpihan Salju Koch

…

Pada Serpihan Salju Koch, setiap titik memilikirank 0, tetapi bukan titik sudut! Serpihan SaljuKoch tidak mempunyai sisi maupun titik sudut!


Georg Cantor:The essence of mathematics is its freedom!

TERIMA KASIH ATAS PERHATIANNYA!


Materi presentasi ini dicuplik dandikembangkan dari buku “Lingkaran: Menguak Misteri Bilangan π, Bangun

Datar dan Bangun Ruang Terkaitdengan Lingkaran” (Graha Ilmu, 2015)

*Istilah Before Calculator dan After Decimals digunakan oleh E. Bombieri & A.J. van der Poorten

Kuliah Umum: LINGKARAN DAN SEGI TAK TERHINGGA

Documents

Transcript of Kuliah Umum: LINGKARAN DAN SEGI TAK TERHINGGA