X

Y

r

Geometri Analitik

BAB XI

LINGKARAN

61. Definisi dan persamaan dari lingkaran. Lingkaran adalah tempat kedudukan yang tetap

dari titik P yang berpindah, oleh karena itu jarak dari sebuah titik tetap adalah konstan/tidak

berubah. Titik tetap itu disebut pusat dan jarak

tetapnya disebut jari-jari.

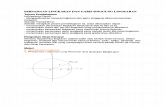
Koordinat dari perpindahan titik P kita bisa

menyebutnya (x , y) . Koordinat dari titik pusat (

α ,β) dan jari-jari r, seperti yang ditunjukkan pada

Gambar 61. Kita ingin mencari persamaan

lingkaranya.

Selama jarak dari (α ,β) ke (x,y) =r

Karena itu :

√ ( x−α )2+ ( y−β )2=r

Atau :

Persamaan ini adalah persamaan lingkaran dengan pusat (α ,β) dan dengan jari-jari r

Itu akan berbeda apabila pusatnya adalah titik pangkalnya (0,0), persamaanya menjadi :

x2+ y2=r2

Contoh

Tentukan pusat dan jari-jari lingkaran dengan persamaan sebagai berikut :

x2+ y2−2 x+4 y−3=0

Kita ingin merubah persamaan ini menjadi bentuk :

( x−α )2+( y−β )2=r 2

Lengkapi persamaan kuadratnya,kita peroleh :

x2−2 x+1+ y2+4 y+4=3+1+4

Atau :

( x−1 )2+( y+2 )2=8

Oleh karena it kita peroleh :Lingkaran

( x−α )2+( y−β )2=r 2

Geometri Analitik

α=1,

β=−2,

r=√8,

Atau :

pusat : (1 ,−2 ) ,

jari− jari :√8

Soal

1. Tentukan pusat dan jari-jari dari beberapa lingkaran, dengan persamaan sebagai berikut :

a) x2+ y2−4 x+2 y−3=0

b) x2+ y2+6 x−8 y−5=0

c) x2+ y2+x−2 y−1=0

d) 3 x2+3 y2+6 x−4 y+2=0

e) 5 x2+5 y2−6 x−2 y+7=0

2. Tentukan persamaan lingkaran sebagai berikut :

a) dengan pusat (2,-1) dan jari-jari = 4

b) dengan pusat (-3,4) dan jari-jari √6

3. Tentukan persamaan lingkaran dengan pusat (2 ,-1) , dan menyinggung sumbu y

4. Tentukan persamaan lingkaran yang mempunyai pusat (-1,4) dan melalui titik (3,5)

5. Tentukan persamaan lingkaran yang diameternya merupakan garis penghubung dari titik

(3,-1) dan (2,5)

6. Tentukan persamaan lingkaran yang mempunyai pusat (-1,3) dan melalui titik (2,7)

7. Tentukan persamaan lingkaran dengan pusat (5,5) dan menyinggung sumbu x

8. Tentukan persamaan lingkaran dengan pusat (1,3) dan menyinggung garis 3 x−4 y−10=0

9. Tentukan persamaan lingkaran dengan pusat (1,-2) dan menyinggung garis x+ y−6=0

10. Tentukan persamaan lingkaran dengan jari - jari 5, dan menyinggung garisx−2 y+6=0

pada (-4,1).

11. Buktikan dengan koordinat bahwa sudut yang tertulis dalam setengah lingkaran adalah

sudut siku-siku.

62. Bentuk umun persamaan lingkaran. Pada bagian 57, kita membuktikan bahwa garis

lurus selalu diwakili oleh sebuah persamaan x dan y, bahwa kebalikan dari teorema ini juga

benar. Kita sekarang akan membahas teorema yang sesuai dengan lingkaran.

Pengembangan

Lingkaran

Geometri Analitik

(1)(x−a)2+( y−ß)2=r2

Dan mengambil hubungan ,kita dapatkan:

x2+ y2−2 αx−2ßy+α2+β2−r2=0

Persamaan ini mungkin dapat ditulis:

(2)x 2+ y 2+Dx+Ey+F=0

Selain itu, D,E, and F adalah konstanta bilangan bulat tetapi bukan bilangan bulat yang perlu.

Dari contoh, berikut ini adalah persamaan dari lingkaran dengan pusat di ( 12

,−1 ) dan dengan

jari - jari 2:

(x−12 )

2

+( y+1 )2=4 ,

Atau

x2+ y2−x+2 y−114

=0

Di sini

D = -1

E = 2,

F = −11

4

Karena setiap lingkaran mempunyai pusat dan jari -jari dan karena lingkaran dengan

memberikan pusat dan memberikan jari - jari yang memiliki setiap persamaan khusus (1) atau

persamaan yang sama pada sebuah bentuk yang berbeda (2) hal ini mengikuti bahwa setiap

lingkaran diwakili oleh persamaan dalam bentuk

Dengan demikian, setiap lingkaran diwakili oleh persamaan tingakt kedua pada x dan y,

dengan koefesien kesatuan x2 dan y2 dan bukan dengan hubungan xy.

Lingkaran

x2 + y2 +Dx +Ey + F + 0

Geometri Analitik

Sebaliknya, setiap bentuk persamaan

x2 +y2+Dx+Ey+F=0

diwakili sebuah lingkaran. Maka, dengan mengkuadratkan, kita mempunyai :

x2+ Dx+( D2 )

2

+ y2+Ey+( E2 )

2

=( D2 )

2

+(E2 )

2

−F ,

Atau

(x+ D2 )

2

+( y+ E2 )

2

=D2+E2−4 F4

.

Persamaan terakhir ini adalah bentuknya

(x−a)2+( y−ß)2=r2

Amatilah, bahawa jika hasilnya menjadi lingkaran yang benar, maka jumlahnya

D2+E2−4 F4

=r 2

haruslah positif. Jika jumlahnya negatif, r adalah bilangan imajiner- yaitu r adalah

akar kuadrat dari angka negatif, dan jika jumlahnya nol, r adalah nol. Karena itu, sebagai

konsekuensinya, kita mengatakan bahwa persamaan dengan imaginari r mewakili lingkaran

imajiner; dan persamaan dengan r sama dengan nol mewakili lingkaran titik.

Contoh berikut menggambarkan prinsip-prinsip yang diberikan di atas.

Contoh

Tentukan persamaan lingkaran yang melalui tiga titik (0,2),(3,3) dan (-1,1).

Persamaan yang ditetapkan akan menjadi bentuk

(2 ) x2+ y2+Dx+Ex+F=0

Karena itu, karena tiga titik terletak pada lingkaran, koordinat nya harus memenuhi

persamaan lingkaran. Sehingga kita memiliki:

(3 ) 0+4+0 . D+2 E+F=0

(4 ) 9+¿

Lingkaran

Geometri Analitik

(5 ) 1+1−D+E+F=0

Penyelesaian tiga persamaan – persamaan tersebut untuk D, E, dan F, kita mendapatkan:

D=−6 ,

E=4 ,

F=−12.

Oleh karena itu persamaan yang ditetapkan adalah:

x2+ y2−6 x+4 y−12=0.

Ada cara penyelesaian lain, yang tidak bergantung pada bentuk (2). Cara ini diilustrasikan

seperti berikut ini:

Contoh

Kita perrtama kali harus mengetahui pusatnya. Dari ilmu ukur bidang, pusatnya adalah titik

potong pembagi dua ruas garis yang tegak lurus yang menghubungkan satu atau beberapa

pasang titik. Dengan cara Bagian 51, persamaan pembagi dua ruas garis yang tegak lurus

yang menghubungkan (0,2) dan (3,3) adalah :

√ x2+( y−2)2=√(x−3)2+( y−3)2 ,

atau:

(6 )3 x+ y−7=0.

Dengan cara yang sama, persamaan pembagi dua ruas garis yang tegak lurus yang

menghubungkan (0,2) dan (-1,1) adalah :

√ x2+( y−2)2=√(x+1)2+( y−1)2 ,

(7 ) x+ y−1=0.

Penyelesaian dari (6) dan (7), kita mendapatkan:

x=3

x=−2

Lingkaran

Geometri Analitik

Karena itu pusatnya pada titik (3, -2). Jarak dari pusat ke satu atau beberapa dari tiga titik

diketahui adalah 5. Oleh karena itu persamaan yang ditetapkan adalah :

(x−3)2+( y+2)2=25 ,

Atau:

x2+ y2−6 x+4 y−12=0.

Permasalahan – permasalahan

1. Tentukan persamaan lingkaran yang melalui titik – titik berikut ini:

a) (2,1), (-1,3), (3,-2).

b) (1,10, (0,6), (2,-3).

c) (-2,1), (1,-4), (3,-1).

2. Tentukan persamaan lingkaran yang mempunyai pusat pada garis x−2 y+3 0 , dan

melalui titik (1,1) dan (0,-3).

3. Tentukan persamaan lingkaran dengan pusat pada (-3,2), dan menyinggung garis

3 x−4 y−3=0.

4. Tentukan persamaan lingkaran dangan jari – jari 5, dan menyinggung garis

2 x− y+4=0 pada (1,6).

5. Tentukan persamaan lingkaran yang menyinggung garis x+ y+2=0 pada (1,1), dan

melalui (2,4).

6. Tentukan persamaan lingakran yang menyinggung 2 x+ y−4=0 pada (2,0), dan

melalui (3,-4).

7. Tentukan persamaan lingkaran yang melalui (2,4) dan (-1,3) dan memiliki pusat pada

garis x−3 y+6=0.

8. Tentukan persamaan lingkaran yang menyinngung 2 x− y+6=0 dan 2 x− y+10=0,

dan memiliki pusat pada garis x−3 y+4=0.

9. Tentukan persamaan lingkaran yang menyinggung x+ y−3=0 dan x=Y +7=0, dan

memiliki pusat pada garis 2 x+ y−4=0.

10. Tentukan persamaaan lingkaran dengan pusat pada sumbu x, dan menyinggung garis

y=4 dan x=2.

11. Tentukan persamaan lingkaran yang pusatnya y=2 dan menyinggung garis

2 x−3 y−4=0 dan x− y−6=0.

12. Tentukan persamaan lingkaran yang menyinggung di titik x=0 , y=0 dan x=5.

Lingkaran

Geometri Analitik

13. Tentukan persamaan lingkaran di dalam sebuah segitiga yang menyinggung garis

3 x−4 y−19=0 ,4 x+3 y−17=0 , dan x−7=0.

14. Tentukan persamaan lingkaran d dalam sebuah segitiga dengan titik puncak (0,6),

(8,6), dan (0,0).

15. Tentukan persamaan lingkaran yang melalui (1,7) dan (8,8) dan menyinggung garis

3 x+4 y−6=0.

63. Lingkaran-lingkaran melalui titik-titik potong dua lingkaran; sumbu radikal.

Pada bagain 60, kita menentukan persamaan lingkaran dari garis yang melalui titik-

titik potong dua lingkaran. Kita dapat menggunakan hal yang sama pada lingkaran dengan

persamaan:

(1)x2+ y2+ A1 x+B1 y+C1=0

(2)x2+ y2+ A2 x+B2 y+C2=0

Kita ingin menunjukkan bahwa persamaan di atas menjadi

(3)x2+ y2+ A1 x+B1 y+C1+k (x2+ y2+ A2 x+B2 y+C2)=0

Untuk semua nilai k (tak terkecuali), baik lingkaran yang melalui titik-titik potong

(real atau imajiner) dari dua buah lingkaran.

Jika dihubungkan, maka kita akan mendapatkan persamaan:

(4)( x2+ y2 ) (1+k )+x ( A1+k A2 )+ y (B1+k B2 )+C1+k C2=0.

Persamaan ini di dapat dari penggabungan kedua persamaan, untuk semua k kecuali -

1, bentuk dari persamaan lingkaran (bagian 62). Akan kita bahas kemudian.selanjutnya, jika

(x1 , y1) adalah titik potong dari dua buah lingkaran, maka titik tersebut berada pada kedua

lingkaran, dan persamaan (3) menjadi:

0+k ∙ 0 ≡ 0

Karena (x1 , y1) berada pada lingkaran maka diwakili oleh persamaan (3).

Jika diberikan lingkaran-lingkaran non konsentris tetapi tidak berpotongan di titik real,

dengan angka tidak real (x , y ) yang memenuhi semua persamaan kemungkinan bernilai

imajiner, karena, persamaan (3) akan mewakili sebuah lingkaran yang berpotingan di titik

imajiner .

Jika diberikan lingakaran-lingkaran konsentris, dengan nilai-nilai (x , y ) tidak real atau

imajiner, memenuhi semua persamaan; karena, persamaan (3) akan mewakili sebuah

lingkaran konsentris.

Yang menarik adalah ketika k=−1. Akan terbentuk persamaan (4), menjadi:

Lingkaran

Geometri Analitik

x ( A1−A2 )+ y ( B1−B2 )+C1−C2=0.

Ini adalah bentuk persamaan sebuah garis lurus, yang biasa disebut sumbu radikal dari

dua buah lingkaran.

Hal itu sudah sangat jelas bahwa, jika persamaan-persamaan lingkaran-lingkaran

dibentuk dari persamaan (1) dan (2), persamaan dari sumbu radikal diperoleh dengan

mengurangi satu persamaan dengan persamaan yang lain.

Misal, persamaan (1) diwakili oleh S1=0,

dan persamaan (2), diwakili oleh S2=0,

maka persamaan sumbu radikalnya adalah : S1−S2=0,

atau: S1=S2.

Untuk lebih jelasnya lagi bahwa, jika titik dua lingkaran berbeda dipotongkan, maka

sumbu radikalnya adalah common chord.

Sekarang ditentukan 3 lingkaran: S1=0 , S2=0 , dan S3=0. Kita akan menentukan

sumbu radikal dari tiga lingkaran (taken in pairs)bertemu pada satu titik disebut titik tengah.

Persamaan sumbu radikal lingkaran S1 = 0 dan S2 = 0 adalah :

(5) S1 – S2 = 0.

Persamaan sumbu radikal lingkaran S2 = 0 dan S3 = 0 adalah :

(6) S2 – S3 = 0.

Persamaan sumbu radikal lingkaran S1 = 0 dan S3 = 0 adalah :

(7) S1 – S3 = 0.

Akan tetapi, jika kita menjumlahkan persamaan (5) dan (6), kita peroleh, dengan 60

bagian, sebuah garis yang melalui titik potong dari (5) dan (6). Dari sini, dengan

menggabungkan (5) dan (6), kita peroleh :

S1 – S3 = 0.

Tetapi hasilnya sama dengan persamaan (7).

Oleh sebab itu, yang mewakili (7) – yaitu, S1 – S3 = 0, yang mana sumbu radikal yang

ketiga – melalui titik potong dari dua lainnya. Atau, dengan kata lain, ketiga sumbu radikal

bertemu di sebuah titik utama.

Lingkaran

Geometri Analitik

Permasalahan - permasalahan

1. Carilah persamaan lingkaran berikut :

a. Melalui titik potong lingkaran x2 + y2 = 2x dan x2 + y2 = 2y, dan (3, -4).

b. Melalui titik potong x2 + y2 = 25 dan x2 + y2 – 2x + 4y – 6 = 0, dan (1, 2).

c. Melalui titik potong lingkaran x2 + y2 = 16 dan garis x + y = 2, dan (4, -3).

2. Carilah sumbu radikal dari lingkaran x2 + y2 – 4x + 6y – 12 = 0 dan x2 + y2 + 2x - y + 3

= 0.

3. Carilah sumbu radikal dari lingkaran x2 + y2 – x + y – 2 = 0 dan 3x2 + 3y2 + 2x - 3y + 6

= 0.

4. Carilah sumbu radikal dari lingkaran x2 + y2 – 6x - 4y + 9 = 0 dan x2 + y2 = 1.

5. Carilah pusat radikal dari lingkaran x2 + y2 + 2x - y = 0, x2 + y2 + x - y - 1 = 0, dan x2 +

y2 - 4x + 6y - 3 = 0.

6. Carilah pusat radikal dari lingkaran x2 + y2 - x + 3y – 2 = 0, x2 + y2 + 4x - 2y - 3 = 0,

dan x2 + y2 - 2x - 4y - 6 = 0.

7. Dalam kasus apa dua lingkaran tidak mempunyai sumbu radikal?

8. Dalam kasus apa tiga lingkaran tidak mempunyai pusat radikal?

9. Berilah cntoh susunan geometri dari sumbu radikal dua lingkaran yang tidak

berpotongan.

10. Buktikan analisa bahwa sumbu radikal dari dua lingkaran adalah tegak lurus dengan

garis tengahnya.

11. Buktikan analisa bahwa sumbu radikal dari dua lingkaran yang sama adalah garis bagi

tegak lurus dari garis tengahnya.

12. Apakah sumbu radikal dari dua lingkaran yang berjari – jari nol?

13. Dengan menggunakan materi soal nomer 12, buktikan bahwa garis bagi tegak lurus

dari dua sisi segitiga bertebu pada satu titik.

14. Jika P (x1, y1) adalah sebuah titik di luar lingkaran

(x - )2 + (y - )2 – r2 = 0,

Tunjukkan bahwa panjang tangent dari P ke lingkaran dapat dirumuskan

t = (x1 - )2 + (y1 - )2 – r2

15. Dengan menggunakan jawaban dari soal 14, tunjukkan bahwa sumbu radikal dari dua

lingkaran, S1 = 0 dan S2 = 0, diartikan sama dengan tempat sebuah titik P berpindah

sehingga tangent yang digambarkan dari P ke lingkaran, S1 = 0 dan S2 = 0, selalu

sama.

Lingkaran